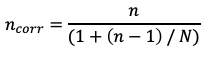Sample Size Calculation: Technical Details Explained Simply

What Is a Representative Sample?

When we conduct a survey to ask about opinions, attitudes, or behavioral patterns, we usually want to find out how common these opinions, attitudes, and behaviors are among the group of people we’re interested in.

These could be, for example, current and/or potential customers of a company, its employees, the residents of a particular city before a mayoral election, or the entire population of a country.

This group of people whose opinion we care about is called the “population.”

In most cases, it is impractical to survey every single person in the population. Aside from the fact that it’s rarely feasible to contact everyone, it would usually be far too expensive and time-consuming.

That’s why researchers began exploring whether and to what extent it’s possible to survey just a small group of people from the population and still obtain answers that are characteristic—i.e., representative—of the entire population.

This subset is called a “sample.” Just like a baker pokes a loaf of bread in different places to check whether it’s baked evenly, statisticians “poke” different parts of the population to see whether the people are similarly “baked.”

In the end, statistics provided an answer to this question—and the answer is both yes and no.

No – because it’s impossible to arrive at exactly the same result as you would get by surveying the entire population.

Yes – because probability theory allows us to estimate how much the true value in the population (e.g., average income or share of people who prefer product X) might deviate from the value obtained through the sample. In other words, it is possible to estimate the interval in which the true value most likely lies.

To calculate this interval, the following conditions must be met:

• Random sampling: Every individual in the population must have an equal chance of being selected for the sample.
• A certain minimum number of people (sample size) must be surveyed.

If these two conditions are met, the sample is considered representative of the population. The insights gained from such a sample can be generalized to the population, and we can estimate how likely it is that we’re making a correct generalization.

How to calculate the sample size—and how to do it yourself—is explained in the next section.

What Happens If the Sample Size Is Chosen Incorrectly?

The consequences of choosing the wrong sample size are quite straightforward:

• If the sample is too small, the survey results cannot be generalized to the population, or the parameters within the population cannot be estimated with the desired precision.
• If the sample is too large, it won’t harm the results, but the data collection costs might be unnecessarily high. This becomes especially noticeable when using panels, where each participant may cost several euros.

The Margin of Error Approach to Calculating Sample Size

Whenever we make statements about a population based on a sample, we introduce an error. This error arises because we only survey a part of the population, not the entire group.

As long as the sample is drawn randomly, we can use probability theory to calculate this error and define the range within which the true value (e.g., the proportion of people answering a question in a certain way) lies in the population.

This range is called the confidence interval and is calculated as “measured value +/- margin of error.”

The formula for calculating the margin of error (for an infinitely large population) is as follows:

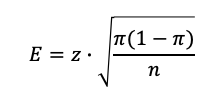(1)

Here,

E – Margin of error (expressed as a decimal).

z – The difference between the value observed in the sample and its theoretical mean, which is the maximum allowable for the chosen confidence level.

The z-score essentially defines the width of the confidence interval, but in terms of the number of standard deviations in the standard normal distribution. The other parameters in the formula translate the z-score into more understandable and interpretable units of allowable percentage deviation.

The z-score for various confidence levels can be found using a z-table.

In survey research, the following confidence levels and corresponding z-scores are typically used:

Confidence Level	z-score
90%	1.65
95%	1.96
99%	2.58

Higher confidence levels correspond to higher z-scores. Therefore, the margin of error increases with higher confidence levels.

π – Proportion of the characteristic in the population (expressed as a decimal). The π value can range from 0% to 100%.

In most cases, the π value is unknown before conducting a survey. In such cases, a value of 50% (0.5) is used. This is because the expression π(1 – π) reaches its maximum at π = 0.5, resulting in the highest possible E value across all possible π values. This ensures that even in worst-case scenarios, the calculated confidence interval includes the true value—or that a sufficiently large sample is selected.

π values that deviate from 0.5 (either upward or downward) produce smaller margins of error. At π = 0 and π = 1, the margin of error is 0.

So, if you know the proportion of the characteristic of interest in your population ahead of the survey, you can significantly reduce the margin of error—and, as we’ll show later, the required sample size—by incorporating this information.

Example:
Your study investigates what proportion of students own a laptop. Since nothing is known about this in your defined population, you use π = 0.5. The results show that 67.5% of respondents answered yes. In a repeat study with the same population, you now use π = 0.675, which reduces the required sample size.

n – Number of respondents, i.e., sample size.

Once we understand all the parameters in the margin of error formula, it’s easy to see that we can rearrange the same formula to calculate the sample size. After a few transformations, the resulting formula looks like this:

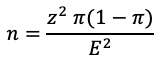(2)

The steps to calculate the sample size are now straightforward:

1. Select the margin of error you want your survey results to have.
2. Select the confidence level for which the survey results should be valid.
3. Determine the z-score that corresponds to your chosen confidence level.
4. If the proportion of the characteristic in the population is known, use it as π. If not, use π = 0.5.
5. Insert the values into formula (2) and calculate the sample size.

This gives you the sample size for the case of an unknown or infinite population.

Sample Size for a Finite Population

It turns out that when the required sample size becomes comparable to the size of the population, smaller samples may already be sufficient to achieve representativeness.

In such cases, the variance of the characteristic not captured by the sample is similar to that captured by it. This allows us to correct the margin of error downward using the so-called Finite Population Correction (FPC) factor:

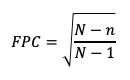(3)

where N stands for the size of the population.

The formula for calculating the margin of error then takes the following form:

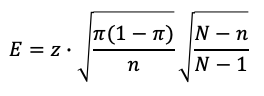(4)

The value of FPC can vary between 0 and 1.

The closer the sample size (n) is to the population size (N), the smaller the FPC becomes. As a result, the margin of error also decreases.

The smaller the sample size relative to the population size, the closer the FPC value approaches 1. In this case, the FPC factor loses relevance, and formula (4) simplifies to formula (1).

The formula for calculating the sample size with FPC—after rearranging formula (4)—looks like this:

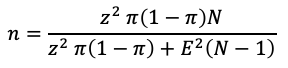(5)

The procedure for calculating the sample size in this case is similar to the approach described in the previous section:

1. Determine the values for E, z, π, and N.
2. Insert them into formula (5).
3. Calculate the required sample size.

Alternatively, and especially helpful when calculating by hand, you can proceed as follows:

1. First calculate the sample size for an infinite population using formula (2).
2. If the calculated sample size exceeds 5% (or at the latest, 10%) of the population size, calculate the corrected sample size using the formula:
   

   (6)

   n_corr is the required sample size.

Example:
We are conducting an employee survey that should be representative of the entire company, with a margin of error of 5% and a confidence level of 95%. According to formula (2), we calculate the required sample size:

n = (1.96^2 * 0.5 * 0.5)/ 0.05^2 = 385.

However, our company has only 100 employees. Therefore, the sample size must be corrected. We calculate the corrected sample size using formula (6):

n_corr = 385 / (1 + (385 – 1)/100) = 80.

In the end, we need to survey 80 employees for the survey to be considered representative of all employees in the company.