2.Survey: Measurement and Scaling

2.1 Introduction

Measurement

Measurement – assigning numbers or other symbols to characteristics of objects according to certain pre-specified rule

– one-to-one correspondence between the numbers and characteristics being measured

– the rules for assigning numbers should be standardized and applied uniformly

– rules must not change over objects or time

 

Scaling

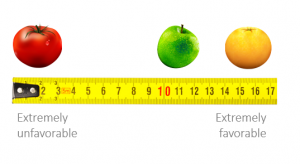
Scaling – involves creating a continuum upon which measured objects are located.

Primary Scales of Measurement

Nominal:

• numbers serve as labels for identifying and classifying objects
• not continuos

Ordinal:

• numbers indicate the relative positions of objects
• but not the magnitude of difference between them

Interval:

• differences between objects can be compared
• zero point is arbitrary

Ratio a.k.a. metric:

• zero point is fixed
• ratios of scale values can be computed

Primary Scales of Measurement

Scale	Basic Characteristics	Common Examples	Marketing Examples	Permissible Statistics
				Descriptive	Inferential
Nominal	Numbers identify and classify objects	Social security numbers, numbering of football players	Brand numbers, store types sex, classification	Percentages, mode	Chi-square, binomial test
Ordinal	Numbers indicate the relative positions of the objects but not the magnitude of differences between them	Quality rankings, ranking of teams in tournament	Preference rankings, market position, social class	Percentile, median	Rank-order correlation, Friedman ANOVA
Interval	Differences between objects can be compared; zero point is arbitrary	Temperature (Fahrenheit, Centigrade)	Attitudes, opinions, index numbers	Range, mean, standard deviation	Product-moment correlations, t-tests, ANOVA, regression, factor analysis
Ratio	Zero point is fixed; ratios of scale values can be compared	Length, weight, time, money	Age, income, costs, sales, market shares	Geometric mean, harmonic mean	Coefficient of variation

 

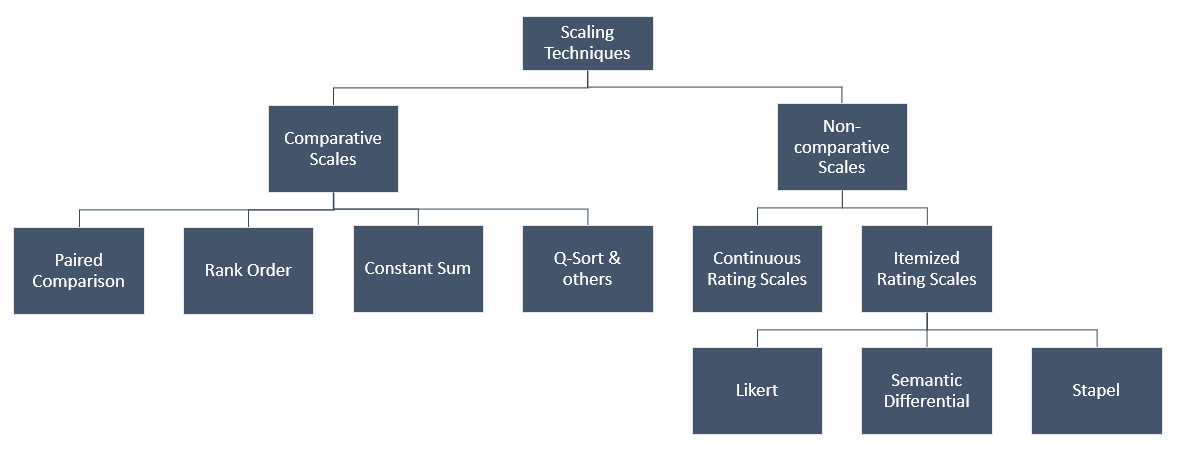
Classification of Scaling Techniques

Comparison of Scaling Techniques

Comparative Scales: 

• involve the direct comparison of stimulus objects.
• data must be interpreted in relative terms
• have only ordinal and rank-order properties

Non-comparative Scales:

• each object is scaled independently
• resulting data is generally assumed to be interval or ratio scaled

– nature of the research

– variability in the population

– statistical considerations

To the table of contents